A Smoother Derivatives Filter Design

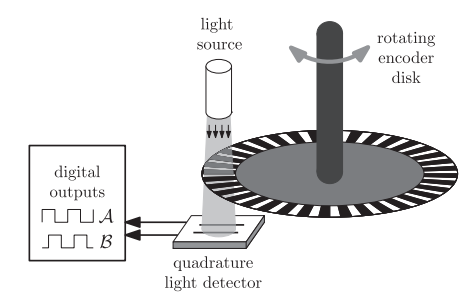
Problem Statement

Usually, we could calulate the first derivative by $$\dot{x} = \frac{x[t]-x[t-dt]}{dt} \hspace{30mm} (1)$$ Below is the raw encoder counts data and the rotation speed (counts/s) calculated by the above equation:

# Import packages
from filterpy.common import Q_discrete_white_noise
from filterpy.kalman import KalmanFilter

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# read data
df = pd.read_csv(r'C:\Users\Abelb\OneDrive - Florida State Students\Attachments\Tallahassee\At FSU\projects\Automation System\Qcar\Sensor_fusion\Data\turn\speed_0_dot_1\turn_0_dot_1.csv',sep=',',header=None)
df = df.values
time = df[:,0]
counts = df[:,11]

# normalization
counts_max = 8390000
d = counts/counts_max
t = time
t.reshape([t.shape[0],1])
d.reshape([t.shape[0],1])

# Calculated first derivative
cal_counts_per_sec = np.zeros(t.shape)
for iter in range(0,d.shape[0]):
    if iter>0:
        dt = time[iter]-time[iter-1]
        cal_counts_per_sec[iter] = counts_max*(d[iter]-d[iter-1])/dt

# Plotting
plt.plot(t, counts,'k', label='Raw counts')
plt.legend()
plt.show()
plt.plot(t, cal_counts_per_sec,'k.', label='calculated counts/second')
plt.legend()
plt.show()

The above figure shows how noisy is the derivative calculated by equation (1) even if the raw data is clean. The noise in derivative is brought by the step time obatined from software timer.
To obtain the clearn and accurate derivative, two filter designs are introduced.

Solution 1: Kalman filter

From the raw data, a quadratic function could be enough to describe the relationship between time and raw counts. Thus, we could assume the acceleration (counts/s^2) is constant governed by noise. The pure state propogation model used in Kalman filter is
$x[k] = x[k-1] + v[k-1]dt$
$ v[k] = v[k-1] + a[k-1]dt \hspace{6mm} (2)$
$ a[k] = a[k-1]$
then the state propogation matrix is $$ F = \begin{bmatrix} 1 & dt & 0 \\ 0 & 1 & dt \\ 0 & 0 & 1 \end{bmatrix}. $$ The measurement is the ecoder counts (x), thus, the measurement matrix is: $$ H = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} $$ The process noise covariance Q and measurement noise R are chosen as follows $$ Q = \begin{bmatrix} 0.01^2 & & \\ & 0.01^2 & \\ & & 0.01^2 \end{bmatrix}, R = 0.15 $$

## Initialization
f = KalmanFilter (dim_x=3, dim_z=1)
f.x = np.array([[0.],    # position
                [0.],    # velocity
                [0.]])   # acceleration
f.H = np.array([[1.,0.,0.]])
f.R = 0.15
dt = 0.1

## perform prediction and update
xs = []
T = []
for iter in range(0,d.shape[0]):
    if iter> 0:
        dt = time[iter]-time[iter-1]
    
    f.F = np.array([[1.,dt,0],
                    [0.,1.,dt],
                    [0.,0.,1.]])
    f.Q = Q_discrete_white_noise(dim=3, dt=dt, var=1e-2)

    z = d[iter]

    f.predict()
    f.update(z)

    states = f.x.copy()

    xs.append(states[1]*counts_max)
    T.append(t[iter])
    
    # print(f.x, 'log-likelihood', f.log_likelihood)
    
## Plotting
plt.plot(t, cal_counts_per_sec,'k.', label='calculated counts/second')
plt.plot(T,xs,'r-',label='KF estimated counts/second')
plt.legend()
plt.show()

Solution 2: Moving-horizon Quadratic filter with low pass filter

As described before, there exist a quadratic relationship between the raw counts data and the time. Instead of assuming the kinematic model in (2), we could designa filter to estimate the parameter of the quadratic function, and output the estimated rotation speed in the meanwhile.
Let’s assume a quadratic function as the local signal model: $$ x(t) = a_0 + a_1 (t - t_{k-1}) + a_2 (t-t_{k-1})^2 \triangleq y(t)^{\top}\theta $$ where $$y(t)=\begin{bmatrix} 1 \\ t-t_{k-1} \\ \left(t-t_{k-1}\right)^{2} \end{bmatrix}, \hspace{2mm} \theta = \begin{bmatrix}a_0 \\ a_1 \\ a_2 \end{bmatrix}.$$ Then the first derivative and second derivative are given as $$ x^{'}(t_k) = a_1+ 2a_2 (t_k - t_{k-1})$$ $$ x^{''}(t_k) = 2a_2 $$ The parameter estimation is given by solving the following optimization program: $$ \hat{\theta}_k = argmin \bigg\{\gamma \|\theta-\theta_{k-1}\|_2^2 + \frac{1}{2}(x_k-y_k^{\top}\theta)^2+\frac{1}{2}(x_{k-1}-y_{k-1}^{\top}\theta)^2 \bigg\}$$ where the first term controls the convergency of parameter $\theta$, the second term and third term are measurement updates on k-1 and k time steps, and $\gamma$ is a forgetting factor.

By solving the above opimization program and give the closed-form solution, then the Algorithm is designed as following:

Algorithm (Moving-horizon Quadratic Filter)

• Inputs:
  $\delta_k : \text{time difference from last observation (time-varying)}$
  $x_k: \text{current measurement} $
  $x_{k-1}: \text{pervious measurement}$
  

• Initilization
  $$\hat{\theta}_0 = \begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix}$$

# Filter initilization
theta_0   = np.zeros([3,1])         # initialization
theta_k_1 = theta_0                 # cache for k-1 parameter theta_{k-1}
x_k_1     = 0
x_hat_low_k_1 = 0 

• Packing data
  $$ y_k^{\star} = \begin{bmatrix}1 & 1 \\ 0 & \delta_k \\ 0 & \delta_k^2 \end{bmatrix}, \hspace{2mm} x_k^{\star} = \begin{bmatrix}x_{k-1}\\ x_k \end{bmatrix}$$
• Computer gain matrix $$ \delta = (\gamma+1)(\gamma+1+\delta_k+\delta_k^2)-1$$ $$D_{k}=\left[\begin{array}{ccc} \frac{1}{\gamma}-\frac{2 \gamma+\delta_{k}+\delta_{k}^{2}}{\gamma \delta} & -\frac{\delta_{k}}{\delta} & \frac{-\delta_{k}^{2}}{\delta} \\
  -\frac{\delta_{k}}{\delta} & \frac{1}{\gamma}-\frac{\delta_{k}^{2}(\gamma+1)}{\gamma \delta} & -\frac{\delta_{k}^{3}(\gamma+1)}{\gamma \delta} \\
  \frac{-\delta_{k}^{2}}{\delta} & -\frac{\delta_{k}^{3}(\gamma+1)}{\gamma \delta} & \frac{1}{\gamma}-\frac{\delta_{k}^{4}(\gamma+1)}{\gamma \delta} \end{array}\right]$$
• update parameter $$ \hat{\theta}_k = D_k\left(\gamma \hat{\theta}_{k-1} + y_k^{\star} x_k^{\star}\right)$$
• Model update
  Filtered measurement $ \hat{x}_k = y(t)^{\top}\hat{\theta}_k $
  Filtered fisrt derivative $ \hat{x}_k^{'} = \begin{bmatrix}0 \\ 1 \\ 2\delta_k\end{bmatrix}\hat{\theta}_k $
  Filtered second derivative $ \hat{x}_k^{''} = \begin{bmatrix}0 \\ 0 \\ 2\end{bmatrix}\hat{\theta}_k$
  

def MH_Quau_filter(Theta_k_1, delta_k, x_k, x_k_1, gamma=1e-4):
    # packing data
    y_k_bar  = np.array([[1, 1], [0, delta_k], [0, delta_k**2]],dtype=object)
    y_k_bar = y_k_bar.reshape((3,2))
    x_k_bar = np.array([x_k_1,x_k],dtype=object).T
    x_k_bar = x_k_bar.reshape((2,1))
    
    # computer gain matrix
    delta = (gamma + 1)*(gamma + 1 + delta_k**2 + delta_k**4) - 1
    D_k   = np.array([[1/gamma - (2*gamma+delta_k**2+delta_k**4)/(gamma*delta), -delta_k/delta, -delta_k**2/delta],
        [-delta_k/delta, 1/gamma - delta_k**2*(gamma+1)/(gamma*delta), -delta_k**3*(gamma+1)/(gamma*delta)],
        [-delta_k**2/delta, -delta_k**3*(gamma+1)/(gamma*delta), 1/gamma - delta_k**4*(gamma+1)/(gamma*delta)]])
    
    # update parameter
    Theta_k = np.dot(D_k,(gamma * Theta_k_1 + np.dot(y_k_bar,x_k_bar)))
    
    # 4. Output
    x_k_hat    = np.dot(np.array([1, delta_k, delta_k**2],dtype=object), Theta_k);  # filtered measurement
    x_k_d_hat  = np.dot(np.array([0, 1, 2*delta_k],dtype=object),Theta_k);          # filtered derivative
    x_k_dd_hat = np.dot(np.array([0, 0, 2],dtype=object),Theta_k);                  # filtered second derivative
    
    return Theta_k, x_k_hat, x_k_d_hat, x_k_dd_hat

## perform prediction and update

# (1) loop Initialization
counts_estimate = np.zeros(d.shape)
counts_per_sec1 = np.zeros(d.shape)  # cache for "without low pass filter"
counts_per_sec2 = np.zeros(d.shape)  # cache for "with low pass filter"

t_previous = 0

tau=1e-1         # Low-pass filter time constant (cutt-off frequency = 1/tau)
gamma = 1e-4     # fogetting factor
    
for iter in range(0,d.shape[0]):
    # (2) signal input
    delta_k = t[iter] - t_previous
        
    # (3) call filter
    Theta_k, x_k_hat, x_k_d_hat, x_k_dd_hat = MH_Quau_filter(theta_k_1, delta_k, d[iter], x_k_1, gamma=gamma)
    
    # (4) Low-pass filter
    x_k_d_low = (1-delta_k/tau) * x_hat_low_k_1 + (delta_k/tau) * x_k_d_hat
    
    counts_estimate[iter] = x_k_hat   * counts_max
    counts_per_sec1[iter] = x_k_d_hat * counts_max
    counts_per_sec2[iter] = x_k_d_low * counts_max
    
    # (5) update cache
    theta_k_1 = Theta_k
    t_previous = t[iter]
    x_k_1 = d[iter]   
    x_hat_low_k_1 = x_k_d_low

# (6) local plotting
plt.plot(t, cal_counts_per_sec,'k.', label='calculated counts/second')
plt.plot(t,counts_per_sec1, label='without low pass filter')
plt.plot(t,counts_per_sec2, label='with low pass filter')
plt.legend()
plt.title('Moving-horizon quadratic filter')
plt.show()

Compare results

plt.plot(t, cal_counts_per_sec,'k.', label='calculated')
plt.plot(T,xs,'r-',label='Kalman filter')
plt.plot(t,counts_per_sec2, label='MH_quau_with_low_pass')
plt.legend()
plt.title('counts/second')
plt.show()

Compared to Kalman filter, the moving-horizon quadratic filter has smaller peak oscillation at the beginning of stable status.